2. Layer Normalization¶
Layer normalization was introduced by Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffery E. Hinton in their 2016 paper Layer Normalization, but it only got really popular after being used in the hugely successful Transformer architecture.
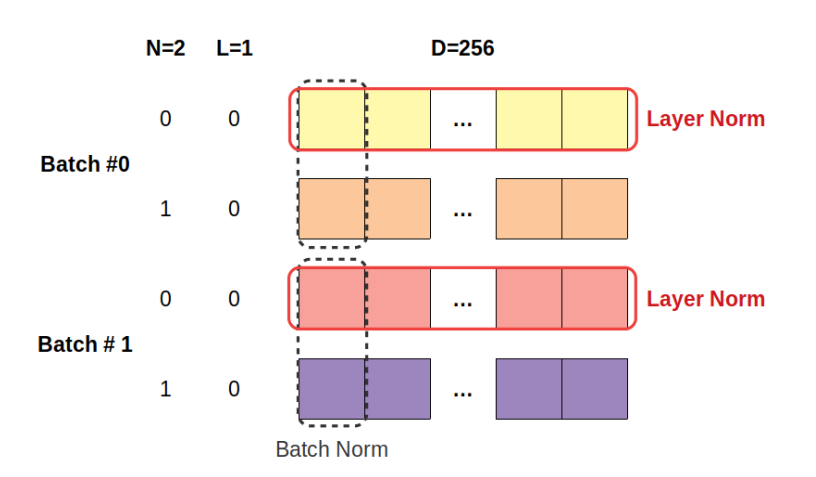
Simply put: layer normalization standardizes individual data
points, not features. This is completely different than the standardizations we’ve performed so far. Before, each feature, either in the whole training set (using Scikit-learn’s StandardScaler or in a mini-batch (using batch norm), was standardized to have zero mean and unit standard deviation. In a tabular dataset, we were standardizing the columns.
Important
Layer normalization Layer normalization, in a tabular dataset, standardizes the rows. Each data point will have the average of its features equals zero, and the standard deviation of its features equals one.
2.1. imports¶
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
2.2. Positional Encoding¶
class PositionalEncoding(nn.Module):
def __init__(self, max_len, d_model):
super().__init__()
self.d_model = d_model
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).float().unsqueeze(1)
angular_speed = torch.exp(torch.arange(0, d_model, 2).float() * (-np.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * angular_speed) # even dimensions
pe[:, 1::2] = torch.cos(position * angular_speed) # odd dimensions
self.register_buffer('pe', pe.unsqueeze(0))
def forward(self, x):
# x is N, L, D
# pe is 1, maxlen, D
scaled_x = x * np.sqrt(self.d_model)
encoded = scaled_x + self.pe[:, :x.size(1), :]
return encoded
2.3. Step-by-step Layer Normalization¶
Calculating the mean of data point
Calculating the standard deviation of the data point
Computing the standardized data point
d_model = 4
seq_len = 2
n_points = 3
torch.manual_seed(34)
data = torch.randn(n_points, seq_len, d_model)
pe = PositionalEncoding(seq_len, d_model)
inputs = pe(data)
inputs
tensor([[[-3.8049, 1.9899, -1.7325, 2.1359],
[ 1.7854, 0.8155, 0.1116, -1.7420]],
[[-2.4273, 1.3559, 2.8615, 2.0084],
[-1.0353, -1.2766, -2.2082, -0.6952]],
[[-0.8044, 1.9707, 3.3704, 2.0587],
[ 4.2256, 6.9575, 1.4770, 2.0762]]])
inputs_mean = inputs.mean(axis=2).unsqueeze(2)
inputs_mean
tensor([[[-0.3529],
[ 0.2426]],
[[ 0.9496],
[-1.3038]],
[[ 1.6489],
[ 3.6841]]])
inputs_var = inputs.var(axis=2, unbiased=False).unsqueeze(2)
inputs_var
tensor([[[6.3756],
[1.6661]],
[[4.0862],
[0.3153]],
[[2.3135],
[4.6163]]])
(inputs - inputs_mean)/torch.sqrt(inputs_var+1e-5)
tensor([[[-1.3671, 0.9279, -0.5464, 0.9857],
[ 1.1953, 0.4438, -0.1015, -1.5376]],
[[-1.6706, 0.2010, 0.9458, 0.5238],
[ 0.4782, 0.0485, -1.6106, 1.0839]],
[[-1.6129, 0.2116, 1.1318, 0.2695],
[ 0.2520, 1.5236, -1.0272, -0.7484]]])
layer_norm = nn.LayerNorm(d_model)
layer_norm.state_dict()
OrderedDict([('weight', tensor([1., 1., 1., 1.])),
('bias', tensor([0., 0., 0., 0.]))])
2.4. PyTorch’s nn.LayerNorm function¶
layer_norm = nn.LayerNorm(d_model)
normalized = layer_norm(inputs)
normalized[0][0].mean(), normalized[0][0].std(unbiased=False)
(tensor(-1.4901e-08, grad_fn=<MeanBackward0>),
tensor(1.0000, grad_fn=<StdBackward>))
layer_norm.state_dict()
OrderedDict([('weight', tensor([1., 1., 1., 1.])),
('bias', tensor([0., 0., 0., 0.]))])
2.5. Layer Normalization of Positionally Encoded Dummy¶
The size of the mini-batch strongly impacts the running statistics of the batch normalization. We also learned that batch norms oscillating statistics may introduce a regularizing effect.
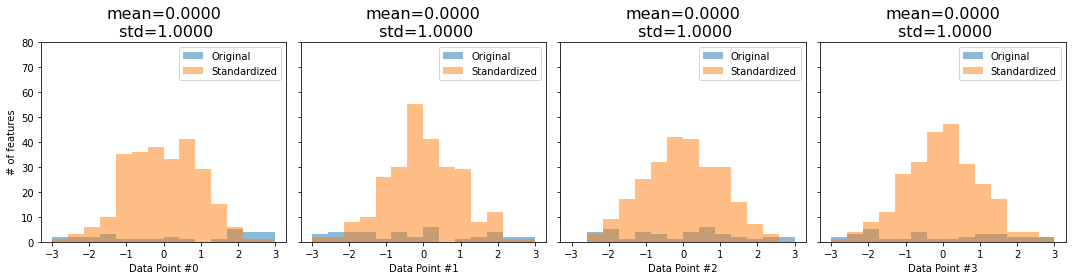
None of this happens with layer normalization: it steadily delivers data points with zero mean and unit standard deviation regardless of our choice of mini-batch size or anything else.
torch.manual_seed(23)
dummy_points = torch.randn(4, 1, 256)
dummy_pe = PositionalEncoding(1, 256)
dummy_enc = dummy_pe(dummy_points)
dummy_enc
tensor([[[-14.4193, 10.0495, -7.8116, ..., -15.4844, -18.0732, -3.9566]],
[[ 2.6628, -3.5462, -23.6461, ..., -0.9403, -18.4375, -37.4197]],
[[-24.6397, -1.9127, -16.4244, ..., -17.3708, -26.0550, -14.0706]],
[[ 13.7988, 21.4612, 10.4125, ..., -3.2333, -17.0188, 3.9237]]])
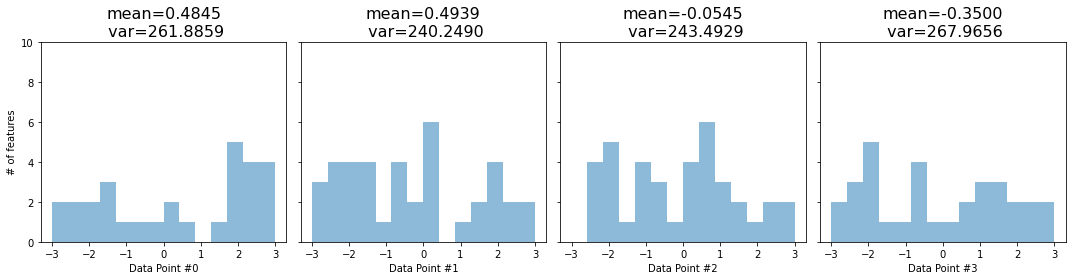
def hist_encoding(encoding):
encoding = encoding.cpu().detach().numpy()
fig, axs = plt.subplots(1, 4, figsize=(15, 4))
axs = axs.flatten()
for i in range(4):
data_point = encoding[i][0]
axs[i].hist(data_point, bins=np.linspace(-3, 3, 15), alpha=.5)
axs[i].set_xlabel(f'Data Point #{i}')
axs[i].set_ylabel('# of features')
axs[i].set_title(f'mean={data_point.mean():.4f}\n var={data_point.var():.4f}', fontsize=16)
axs[i].set_ylim([0, 10])
axs[i].label_outer()
fig.tight_layout()
return fig
def hist_layer_normed(encoding, normed):
encoding = encoding.cpu().detach().numpy()
normed = normed.cpu().detach()
fig, axs = plt.subplots(1, 4, figsize=(15, 4))
for i in range(4):
data_point = encoding[i][0]
normed_point = normed.detach()[i][0]
axs[i].hist(data_point, bins=np.linspace(-3, 3, 15), alpha=.5, label='Original')
axs[i].hist(normed_point.numpy(), bins=np.linspace(-3, 3, 15), alpha=.5, label='Standardized')
axs[i].set_xlabel(f'Data Point #{i}')
axs[i].set_ylabel('# of features')
axs[i].set_title(f'mean={normed.mean().numpy():.4f}\n std={normed.std(unbiased=False).numpy():.4f}', fontsize=16)
axs[i].legend()
axs[i].set_ylim([0, 80])
axs[i].label_outer()
fig.tight_layout()
return fig
fig = hist_encoding(dummy_enc)
layer_normalizer = nn.LayerNorm(256)
dummy_normed = layer_normalizer(dummy_enc)
dummy_normed
tensor([[[-0.9210, 0.5911, -0.5127, ..., -0.9868, -1.1467, -0.2744]],
[[ 0.1399, -0.2607, -1.5574, ..., -0.0925, -1.2214, -2.4460]],
[[-1.5755, -0.1191, -1.0491, ..., -1.1097, -1.6662, -0.8982]],
[[ 0.8643, 1.3324, 0.6575, ..., -0.1761, -1.0183, 0.2611]]],
grad_fn=<NativeLayerNormBackward>)
fig = hist_layer_normed(dummy_enc, dummy_normed)
2.6. Our Seq2Seq Problem¶
So far, we have been using dummy examples to illustrate how layer normalization works. Let’s go back to our sequence-to-sequence problem, where the source sequence had two data points, each data point representing the coordinates of two corners. As usual, we are adding positional encoding to it
pe = PositionalEncoding(max_len=2, d_model=2)
source_seq = torch.tensor([[[ 1.0349, 0.9661], [ 0.8055, -0.9169]]])
source_seq_enc = pe(source_seq)
source_seq_enc
tensor([[[ 1.4636, 2.3663],
[ 1.9806, -0.7564]]])
norm = nn.LayerNorm(2)
norm(source_seq_enc)
tensor([[[-1.0000, 1.0000],
[ 1.0000, -1.0000]]], grad_fn=<NativeLayerNormBackward>)
Warning
When one tries to layer normalize two features only: they become either minus one or one. Even worse, it will be the same for every data point. These values will not get us anywhere.
We need projections (for numerical values) or embeddings (for categorical values) to get us from 2 dimensions to a different dimensionality.
2.7. Projections or Embeddings¶
Note
Sometimes projections and embeddings are used interchangeably. Here, we are sticking with embeddings for categorical values and projections for numerical values. }
Projections/Embeddings are referring to using a simple linear layer to project our pair of coordinates into a higher-dimensional feature space.
torch.manual_seed(11)
proj_dim = 6
linear_proj = nn.Linear(2, proj_dim)
pe = PositionalEncoding(2, proj_dim)
source_seq_proj = linear_proj(source_seq)
source_seq_proj_enc = pe(source_seq_proj)
source_seq_proj_enc
tensor([[[-2.0934, 1.5040, 1.8742, 0.0628, 0.3034, 2.0190],
[-0.8853, 2.8213, 0.5911, 2.4193, -2.5230, 0.3599]]],
grad_fn=<AddBackward0>)
norm = nn.LayerNorm(proj_dim)
norm(source_seq_proj_enc)
tensor([[[-1.9061, 0.6287, 0.8896, -0.3868, -0.2172, 0.9917],
[-0.7362, 1.2864, 0.0694, 1.0670, -1.6299, -0.0568]]],
grad_fn=<NativeLayerNormBackward>)
